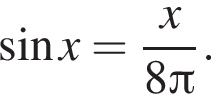1. Задание № 237 

Сложность: IV
Классификатор алгебры: 6\.5\. Тригонометрические уравнения вида f(x)=f(y)
Методы алгебры: Использование косвенных методов
Уравнения смешанного типа, разные вопросы об уравнениях
i
Найдите количество корней уравнения 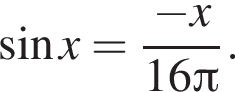
Решение. Чтобы уравнение имело решение необходимо: 
В точке ![]() уравнение имеет 1 корень. На отрезке
уравнение имеет 1 корень. На отрезке ![]() уравнение будет иметь 2 корня. Заметим, что на каждом из отрезков
уравнение будет иметь 2 корня. Заметим, что на каждом из отрезков 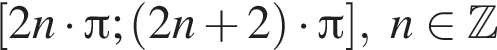 вплоть до
вплоть до ![]() уравнение будет иметь два корня. В точке
уравнение будет иметь два корня. В точке 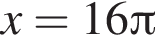 решений нет. Поэтому на положительной полуоси уравнение имеет 16 решений. На отрицательной полуоси будет столько же решений. Итого имеем 33 решения.
решений нет. Поэтому на положительной полуоси уравнение имеет 16 решений. На отрицательной полуоси будет столько же решений. Итого имеем 33 решения.
Ответ: 33.
Ответ: 33
237
33
Сложность: IV
Классификатор алгебры: 6\.5\. Тригонометрические уравнения вида f(x)=f(y)
Методы алгебры: Использование косвенных методов
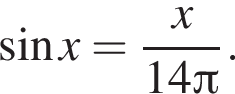

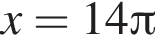 уравнение корней не имеет. Поэтому на положительной полуоси уравнение имеет 13 решений. На отрицательной полуоси будет столько же решений. Итого имеем 27 решений.
уравнение корней не имеет. Поэтому на положительной полуоси уравнение имеет 13 решений. На отрицательной полуоси будет столько же решений. Итого имеем 27 решений.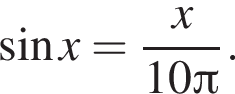

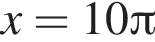 уравнение корней не имеет. Поэтому на положительной полуоси уравнение имеет 9 решений. На отрицательной полуоси будет столько же решений. Итого имеем 19 решений.
уравнение корней не имеет. Поэтому на положительной полуоси уравнение имеет 9 решений. На отрицательной полуоси будет столько же решений. Итого имеем 19 решений.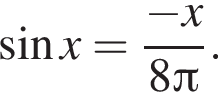
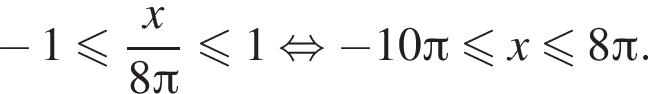
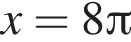 уравнение корней не имеет. Поэтому на положительной полуоси уравнение имеет 8 решений. На отрицательной полуоси будет столько же решений. Итого имеем 17 решений.
уравнение корней не имеет. Поэтому на положительной полуоси уравнение имеет 8 решений. На отрицательной полуоси будет столько же решений. Итого имеем 17 решений.